Question

A planet orbits a star, in a year of length 2.27 x 107 s, in a nearly circular orbit of radius 3.99 x 1011 m. With respect to the star, determine (a) the angular speed of the planet, (b) the tangential speed of the planet, and (c) the magnitude of the planet's centripetal acceleration.

Answer 1

Step-by-step explanation:

It is given that,

Radius of circular orbit,
`r=3.99* 10^(11)\ m`

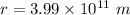
Time taken,
`t=2.27* 10^(7)\ m`

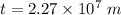
(a) Angular speed of the planet is given by :

`\omega=(2\pi)/(t)`

`\omega=(2\pi)/(2.27* 10^(7)\ m)`

`\omega=2.76* 10^(-7)\ rad/s`

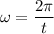
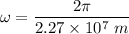
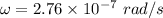
(b) The tangential speed of the planet is given by :

`v=r* \omega`

`v=3.99* 10^(11)* 2.76* 10^(-7)`

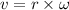
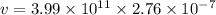
v = 110124 m/s

(c) The centripetal acceleration of the planet,

`a=(v^2)/(r)`

`a=((110124)^2)/(3.99* 10^(11))`

`a=0.0303\ m/s^2`

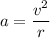
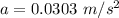
Hence, this is the required solution.