Answer:
The radius of the solenoid is 0.94 meters.
Step-by-step explanation:
It is given that,
The magnetic field strength within the solenoid is given by the equation as :
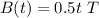
Where
t is the in seconds
The induced electric field outside the solenoid is,
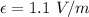
Distance, d = 2 m from the axis of the solenoid
To find,
The radius of the solenoid.
Solution,
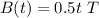
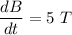
The expression for the induced emf is given by :
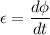
 = magnetic flux
= magnetic flux
The electric field due to changing magnetic field is given by :


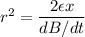
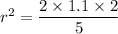
r = 0.9380 m
or
r = 0.94 meters
So, the radius of the solenoid is 0.94 meters. Hence, this is the required solution.