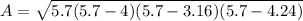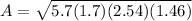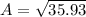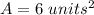Question

Triangle ABC has vertices at A(-2,1), B(-2,-3), and C(1,-2). What is the area of the triangle? a 18 square units b 9 square units c 6 square units d 12 square units

Answer 1

Option C. 6 square units

Explanation:

we know that

Heron's Formula is a method for calculating the area of a triangle when you know the lengths of all three sides.

Let

a,b,c be the lengths of the sides of a triangle.

The area is given by:

`A=√(p(p-a)(p-b)(p-c))`

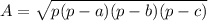
where

p is half the perimeter

p=
`(a+b+c)/(2)`

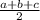
we have

Triangle ABC has vertices at A(-2,1), B(-2,-3), and C(1,-2)

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

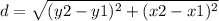
step 1

Find the distance AB

`d=\sqrt{(-3-1)^(2)+(-2+2)^(2)}`

`d=\sqrt{(-4)^(2)+(0)^(2)}`

`dAB=4\ units`

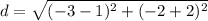
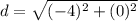
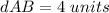
step 2

Find the distance BC

`d=\sqrt{(-2+3)^(2)+(1+2)^(2)}`

`d=\sqrt{(1)^(2)+(3)^(2)}`

`dBC=√(10)\ units`

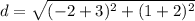
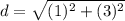
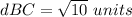
step 3

Find the distance AC

`d=\sqrt{(-2-1)^(2)+(1+2)^(2)}`

`d=\sqrt{(-3)^(2)+(3)^(2)}`

`dBC=√(18)\ units`

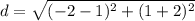
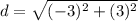
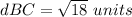
step 4

`a=AB=4\ units`

`b=BC=√(10)\ units`

`c=AC=√(18)\ units`

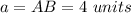
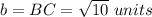
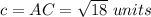
Find the half perimeter p

p=
`(4+√(10)+√(18))/(2)=5.70\ units`

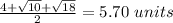
Find the area

`A=√(5.7(5.7-4)(5.7-3.16)(5.7-4.24))`

`A=√(5.7(1.7)(2.54)(1.46))`

`A=√(35.93)`

`A=6\ units^(2)`