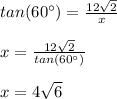Question

See below to answer this question

Answer 1

Answer: OPTION A.

Explanation:

Observe the figure attached.

The first step is the find "a". In order to find this side, we need to use this Trigonometric Identity:

`sin\alpha=(opposite)/(hypotenuse)`

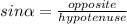
In this case:

`\alpha=45\°\\\\opposite=12\\\\hypotenuse=a`

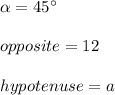
Then, substituting values and solving for "a", we get:

`sin(45 \°)=(12)/(a)\\\\a=(12)/(sin(45 \°))\\\\a=12√(2)`

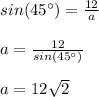
Now we must apply this Trigonometric Identity:

`tan\theta=(opposite)/(adjacent)`

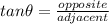
In this case:

`\theta=60\°\\\\opposite=12√(2)\\\\adjacent=x`

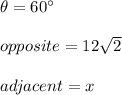
Then, substituting values and solving for "x", we get:

`tan(60\°)=(12√(2))/(x)\\\\x=(12√(2))/(tan(60 \°))\\\\x=4√(6)`

Answer 2

c. 6√2

Explanation:

The step by step explanation is shown in the picture above