Answer : The final volume of air will be 9.366 liters.
Explanation :
First we have to calculate the initial volume of air by using ideal gas law.
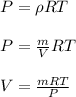
where,
P = initial pressure = 100 kPa = 100000 Pa =

 = density of air
= density of air
m = mass of air = 0.2 kg
R = gas constant = 287 J/kg.K
T = temperature of air = 300 K
V = initial volume of air = ?
Now put all the given values in the above formula, we get:
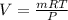
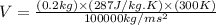
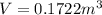
The initial volume of air is,
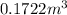
Now we have to calculate the final volume of air by using Boyle's law.
According to the Boyle's law, the pressure of the gas is inversely proportional to the volume of the gas at constant temperature of the gas and the number of moles of gas.

or,
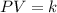
or,
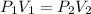
where,
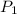 = initial pressure of the gas = 100 kPa = 100000 Pa =
= initial pressure of the gas = 100 kPa = 100000 Pa =

 = final pressure of the gas = 1838.5 kPa = 1838500 Pa =
= final pressure of the gas = 1838.5 kPa = 1838500 Pa =
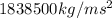
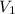 = initial volume of the gas =
= initial volume of the gas =
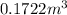
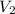 = final volume of the gas = ?
= final volume of the gas = ?
Now put all the given values in this formula, we get the final volume of the air.
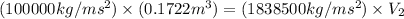
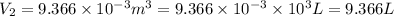
conversion used :
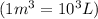
Therefore, the final volume of air will be 9.366 liters.