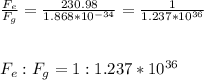Answer:
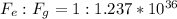
Step-by-step explanation:
Parameters given:
Distance between the protons, r =
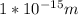
Electric charge of proton, Q =
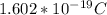
Mass of proton, m =

The electric force on one proton due to the other given as:
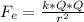
where k = Coulomb's constant
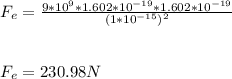
The gravitational force on one proton due to the other is given as:
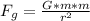
where G = gravitational constant
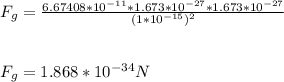
Therefore, the ratio of electric force,
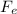 , and gravitational force,
, and gravitational force,
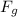 , is:
, is: