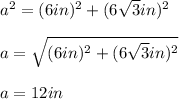Question

Which of these is the length of the hypotenuse of a 30 60 90 triangle with legs measuring 6in and 6 square root of 3in

Answer 1

Answer: The length of the hypotenuse is 12 inches.

Explanation:

In this case we need to use the Pythagorean Theorem. This is:

`a^2=b^2+c^2`

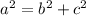
Where "a" is the hypotenuse and "b" and "c" are the legs of the right triangle.

We can say that:

`b=6in\\c=6√(3)in`

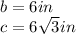
Then, substituting values into
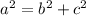`a^2=b^2+c^2` and solving for "a", we get that the lenght of the hypotenuse is the following:

`a^2=(6in)^2+(6√(3)in)^2\\\\a=\sqrt{(6in)^2+(6√(3)in)^2}\\\\a=12in`