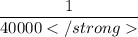Question

The chance that two people both have three repeat sequences at location A is 1 in 500. The chance that two people have four repeat sequences at location B is 1 in 800. What is the probability that two people have the same number of repeats in both location A and location B

Answer 1

Answer: Probability that two people have the same number of repeats in both location A and location B is

Probability that two people both have 4 repeat sequences at location B =
`(1)/(800)`

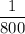
P(A) =
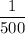`(1)/(500)` and P(B) =
`(1)/(800)`

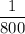
Since A and B are independent events.

According to question,

`P(A\cap B)=P(A).P(B)\\\\P(A\cap B)=(1)/(500)* (1)/(800)\\\\P(A\cap B)=(1)/(40000)`

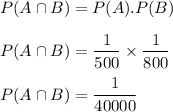
Hence, probability that two people have the same number of repeats in both location A and location B is
`(1)/(40000</strong>)`