Answer : The correct option is, (C) 1.1
Solution : Given,
Initial moles of
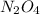 = 1.0 mole
= 1.0 mole
Initial volume of solution = 1.0 L
First we have to calculate the concentration
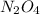 .
.
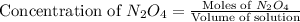
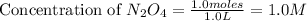
The given equilibrium reaction is,
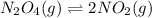
Initially c 0
At equilibrium
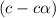
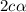
The expression of
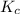 will be,
will be,
![K_c=([NO_2]^2)/([N_2O_4])](https://img.qammunity.org/2020/formulas/physics/college/qjqdoekzbudhpleet02icllsrildnndyp1.png)
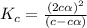
where,
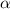 = degree of dissociation = 40 % = 0.4
= degree of dissociation = 40 % = 0.4
Now put all the given values in the above expression, we get:
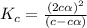
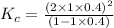
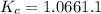
Therefore, the value of equilibrium constant for this reaction is, 1.1