Question

By how much does the volume of an aluminum cube 4.00 cm on an edge increase when the cube is heated from 19.0°C to 67.0°C? The linear expansion coefficient of aluminum is 23.0 x 10^-6 /C°.

Answer 1

The volume of an aluminum cube is 0.212 cm³.

Step-by-step explanation:

Given that,

Edge of cube = 4.00 cm

Initial temperature = 19.0°C

Final temperature = 67.0°C

linear expansion coefficient
`\alpha=23.0*10^(-6)/C^(\circ)`

We need to calculate the volume expansion coefficient

Using formula of volume expansion coefficient

`\beta=3\alpha`

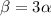
Put the value into the formula

`\beta=3*23.0*10^(-6)`

`\beta=0.000069=69*10^(-6)/C^(\circ)`

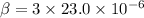
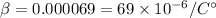
We need to calculate the volume

`V= a^3`

`V=4^3`

`V=64\ cm^3`

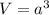
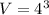
The change temperature of the cube is

`\Delta T=T_(f)-T_(i)`

Put the value into the formula

`\Delta T=67-19 = 48^(\circ)C`

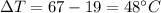
We need to calculate the increases volume

Using formula of increases volume

`\Delta V=V\beta\Delta T`

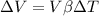
Put the value into the formula

`\Delta V=64*69*10^(-6)*48`

`\Delta V=0.212\ cm^3`

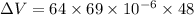
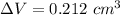
Hence, The volume of an aluminum cube is 0.212 cm³.