Question

An ancient club is found that contains 100 g of pure carbon and has an activity of 6.5 decays per second. Determine its age assuming that in living trees the ratio of (14C/12C) atoms is about 1.30×10^-12. Note that the half life of carbon-14 is 5700 years and the Avogadro number is 6.02×10^23.

Answer 1

The age of living tree is 11104 years.

Step-by-step explanation:

Given that,

Mass of pure carbon = 100 g

Activity of this carbon is = 6.5 decays per second = 6.5 x60 decays/min =390 decays/m

We need to calculate the decay rate

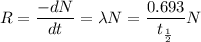`R=(-dN)/(dt)=\lambda N=\frac{0.693}{t_{(1)/(2)}}N`....(I)

Where, N = number of radio active atoms

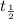`t_{(1)/(2)}`=half life

We need to calculate the number of radio active atoms

For
`N_{12_(c)}`

`N_{12_(c)}=(N_(A))/(M)`

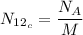
Where,
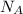`N_(A)` =Avogadro number

`N_{12_(c)}=(6.02*10^(23))/(12)`

`N_{12_(c)}=5.02*10^(22)\ nuclie/g`

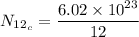
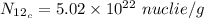
For
`N_{c_(14)}`

`N_{c_(14)}=1.30*10^(-12)N_{12_(c)}`

`N_{c_(14)}=1.30*10^(-12)*5.02*10^(22)`

`N_{c_(14)}=6.526*10^(10)\ nuclei/g`

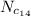
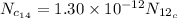
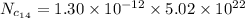
Put the value in the equation (I)

`R=(0.693*6.526*10^(10)*60)/(5700*3.16*10^(7))`

`R=15.0650\ decay/min g`

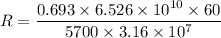
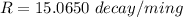
100 g carbon will decay with rate

`R=100*15.0650=1507\ decay/min`

We need to calculate the total half lives

`((1)/(2))^(n)=(390)/(1507)`

`2^n=(1507)/(390)`

`2^n=3.86`

`n ln 2=ln 3.86`

`n=(ln 3.86)/(ln 2)`

`n =1.948`

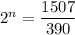
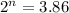
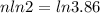
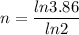
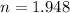
We need to calculate the age of living tree

Using formula of age

`t=n* t_{(1)/(2)}`

`t=1.948*5700`

`t=11103.6 =11104\ years`

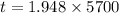
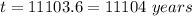
Hence, The age of living tree is 11104 years.