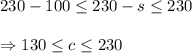Question

You earn $250 per month from your part-time job. You are in a kayaking club that costs $20 per month, and you save at least $100 each month. Write and solve an inequality to find the possible amounts you have left to spend each month

Answer 1

Amounts in the intervall
`130 \leq c \leq 230`

Explanation:

We will take the variables c and s, where

c = amount to spend that month

s = savings of the month.

Since each month we save at least 100, we know that

`0 \leq s \leq 100`

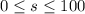
Moreover, we earn $250 per month and we spend $20 in a kayaking club, which tells us that

`250=20+s+c`

and so

`230-s=c`

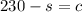
By multiplying by -1, the first inequality also tells us that

`-100 \leq -s \leq 0`

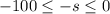
Consequently by adding 230 to the inequality, we get that

`230-100 \leq 230-s \leq 230\\\\\Rightarrow 130\leq c \leq 230`