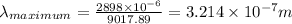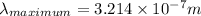Question

Assuming that a given star radiates like a blackbody, estimate the wavelength of its strongest radiation when it emits a total intensity of 375 MWm? (b) Find the temperature at its surface.

Answer 1

a) wavelength,
`\lambda _(maximum) = 3.214* 10^(-7) m`

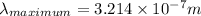
b) Surface temperature, T = 9017.89 K

Given:

Total Intensity, P = 375 MWm = 375
`* 10^(6) Wm`

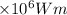
Here, total intensity is the power per unit area

Solution:

a) Using Wien's displacement law which gives the inverse relation between temperature and wavelength for black body radiation and is given by:

`\lambda _(maximum) = (k)/(T)` (1)

where

k = proportionality constant = 2898
`\micro m.K`

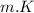
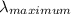`\lambda _(maximum)` = maximum wavelength

T = Temperature in kelvin

From eqn (1):

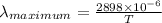`\lambda _(maximum) = (2898* 10^(-6))/(T)` {2}

b) Temperature, T at the surface is given by Stefan-Boltzman law:

P =
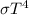`\sigma T^(4)` (3)

where

`\sigma = Stefan-Boltzman = 5.670373* 10^(-8) W/m^(2)K^(4)`

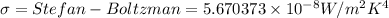
Using eqn (3):

`T^(4) = (P)/(\sigma )`

`T^(4) = (375* 10^(6))/(5.670373* 10^(-8)) = 6.61332* 10^(15)`

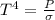
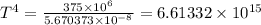
T = 9017.89 K

Now, substituting the value of T = 9017.89 K in eqn (2):

`\lambda _(maximum) = (2898* 10^(-6))/(9017.89) = 3.214* 10^(-7) m`

`\lambda _(maximum) = 3.214* 10^(-7) m`