Answer:
angular frequency of the table must be same as the frequency of the projection of the gum on the wall
Step-by-step explanation:
Since we know that the projection on the wall is the vertical component of the position of the gum on the rotating table
So here we will say
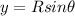
so the angle made by the radius vector depends on the angular frequency of the disc by which it is rotating
So we can say
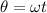
so here we can say
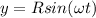
so here we can say that
angular frequency of the table must be same as the frequency of the projection of the gum on the wall