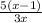Question

What is the simplified form of the rational expression below 5x2-5/3x2+3x

Answer 1

(5(x-1))/3x

Explanation:

Answer 2

`(5(x-1))/(3x)`

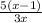
Explanation:

The given expression is

`(5x^(2) -5)/(3x^(2)+3x)`

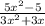
To simplify this rational expression, we need to extract the greatest common factor of each part,

`(5x^(2) -5)/(3x^(2)+3x)=(5(x^(2)-1) )/(3x(x+1))`

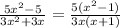
Then, we observe that the numerator has a difference of two perfect squares, which can be factored as

`a^(2) -b^(2) =(a-b)(a+b)`

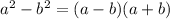
Where,
`a=x` and
`b=1`

`x^(2) -1=(x-1)(x+1)`

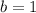
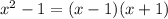
Now, we applied this to the rational expression

`(5x^(2) -5)/(3x^(2)+3x)=(5(x^(2)-1) )/(3x(x+1))=(5(x-1)(x+1))/(3x(x+1))=(5(x-1))/(3x)`

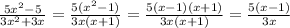
Therefore the simplified form of the given expression is

`(5(x-1))/(3x)`