Question

The sum of the divisors function \sigma (n) is not a multiplicative function.
True
False

Answer 1

True.

Explanation:

If a function is multiplicative then it hold following properties

1.f(1)=1

2.
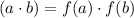`\f(a\cdot b)=f(a)\cdot f(b)` hold for all a and b when even a and b are not co-prime.

Let
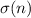`\sigma(n)` is a function of sum of divisor of n

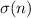`\sigma (n)`=Sum of divisor of n

If n=1 then

`\sigma (1)=1`

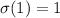
It is satisfied first property.

Suppose n=9

Then divisor of 9=1,3,9

Sum of divisor=1+3+9=13

Divisor of 3=1,3

Sum of divisors of 3=1+3=4

`\sigma (9)=13`

`\sigma (3)\cdot \sigma(3)=4\cdot 4=16`

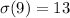
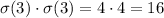
Hence,
`\sigma (a\cdot b)\\eq \sigma(a)\cdot \sigma(b)`

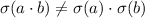
Therefore,
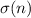`\sigma(n)` is not a multiplicative function.

Hence, given statement is true.