Question

The displacement y is expressed as a function of x and t in terms of the wave numberk and the angular frequency. Write the equivalent equations in which y is shown as a function of x in terms of (a) kand v, (b) 1 and v(c) and fand (d) f and v.

Answer 1

Step-by-step explanation:

The displacement equation is given by :

(a)
`y=A\ sin(\omega t\pm kx)`

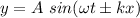
Since,
`\omega=2\pi f`

`\lambda=(2\pi)/(k)`

`y=A\ sin(2\pi f t\pm kx)`

`y=A\ sin((2\pi vt)/(2\pi /k)\pm kx)`

`y=A\ sin(kvt+kx)`

`y=A\ sink(vt+x)`

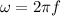
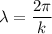
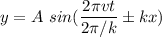
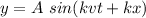
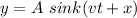
The above equation is in terms of k and v.

(b)
`y=A\ sin(\omega t\pm kx)`

`y=A\ sin(2\pi (v)/(\lambda)t\pm(2\pi)/(\lambda)x)`

`y=Asin(2\pi)/(\lambda)(vt\pm x)`

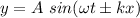
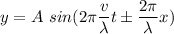
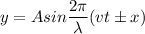
(c)
`y=A\ sin(\omega t\pm kx)`

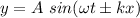
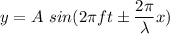
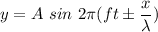
`y=A\ sin(2\pi f t\pm (2\pi)/(\lambda) x)`

`y=A\ sin\ 2\pi (ft\pm (x)/(\lambda))`

(d)
`y=A\ sin(\omega t\pm kx)`

`y=A\ sin(2\pi ft+(2\pi)/(\lambda)x)`

`y=A\ sin(2\pi ft+(2\pi)/(v/f)x)`

`y=A\ sin\ 2\pi f(t+(x)/(v))`

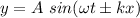
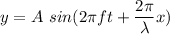
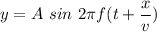
Where

k is the propagation constant

v is the speed of wave

f is the frequency of a wave

`\lambda` is the wavelength

Hence, this is the required solution.