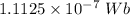Question

The inductance of a closely packed coil of 560 turns is 8.9 mH. Calculate the magnetic flux through the coil when the current is 7.0 mA.

Answer 1

The magnetic flux through the coil is
`1.1125*10^(-7)\ Wb`

Step-by-step explanation:

Given that,

Number of turns = 560

Inductance = 8.9 mH

Current = 7.0 mA

We need to calculate the magnetic flux

Using formula for magnetic flux

`L=(N\phi)/(I)`

`\phi=(LI)/(N)`

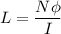
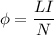
Where, L = inductance

I = current

N = number of turns

Put the value into formula

`\phi=(8.9*10^(-3)*7.0*10^(-3))/(560)`

`\phi=1.1125*10^(-7)\ Wb`

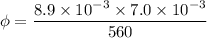
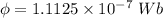
Hence, The magnetic flux through the coil is
`1.1125*10^(-7)\ Wb`

Answer 2

`0.11* 10^(-6)weber`

Step-by-step explanation:

We have given number of turns N = 560

Inductance L = 8.9 mH

Current through the coil = 7 mA

Inductance of the coil is given as
`L=(N\Phi )/(I)`

Where N is number of turns I is current and
`\Phi` is flux

So
`\Phi =(LI)/(N)=(8.9* 10^(-3)* 7* 10^(-3))/(560)=0.11* 10^(-6)weber`