Answer:
The parametric equations for the given line are x=1-t, y=1+t and z=2t.
Explanation:
Given information: P (1,1,0) and Q (0,2,2).
The parametric equation of line are

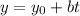
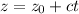
where,
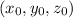 is point on line and <a,b,c> is direction vector.
is point on line and <a,b,c> is direction vector.
The line passes through the points P (1,1,0) and Q (0,2,2). So, the direction vector is

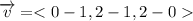
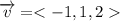
The direction vector is <-1,1,2>. So, a=-1, b=1 and c=2. The parametric equation of line are
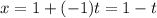
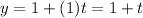
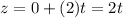
Therefore the parametric equations for the given line are x=1-t, y=1+t and z=2t.