Question

Find the parametric equations for the line that passes through the points P (1,1,0) and Q (0,2,2).

Answer 1

The parametric equations for the given line are x=1-t, y=1+t and z=2t.

Explanation:

Given information: P (1,1,0) and Q (0,2,2).

The parametric equation of line are

`x=x_0+at`

`y=y_0+bt`

`z=z_0+ct`

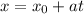
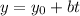
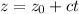
where,
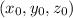`(x_0,y_0,z_0)` is point on line and <a,b,c> is direction vector.

The line passes through the points P (1,1,0) and Q (0,2,2). So, the direction vector is

`\overrightarrow{v}=<x_2-x_1, y_2-y_1, z_2-z_1>`

`\overrightarrow{v}=<0-1,2-1, 2-0>`

`\overrightarrow{v}=<-1,1,2>`

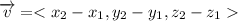
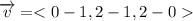
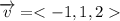
The direction vector is <-1,1,2>. So, a=-1, b=1 and c=2. The parametric equation of line are

`x=1+(-1)t=1-t`

`y=1+(1)t=1+t`

`z=0+(2)t=2t`

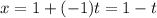
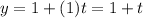
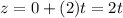
Therefore the parametric equations for the given line are x=1-t, y=1+t and z=2t.