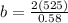Answer:
Part a)
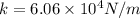
Part b)

Step-by-step explanation:
Part a)
as the mass of the suspension system is given as
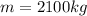
also we have
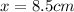
so now for force balance we have

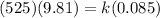
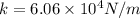
Part b)
Now we know that amplitude decreases by 63% in each cycle
so after one cycle the amplitude will become 37% of initial amplitude
so it is given as
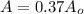
also we know
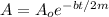
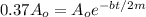
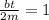
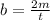
here t = time period of one oscillation
so it is
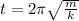
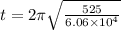

now damping constant is