Answer:
Length of enclosure =18.89 foot
Width of enclosure=11.12 foot
Explanation:
We are given that a fence is to be built to enclose a rectangular area 210 square feet.
Fence along three sides is to be made of material that costs 5 dollars per foot
and the material for the fourth side costs 12 dollars per foot.
We have to find the dimension of the enclosure that is most economical
Let x be the length and y be the width of enclosure
We know that area of rectangle=


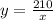
Cost of four sides =
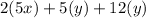
Total cost=
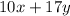
C=

C=

Differentiate w.r.t x

Substitute

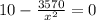
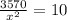
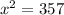
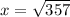
x=18.89
Differentiate w.r.t x
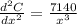
Substitute x=18.89
Then we get
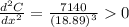
Hence, the cost is minimum.
Length of enclosure =18.89 foot
Width of enclosure=

Hence, the dimension of the enclosure that is most economical to construct
Length=18.89 foot and width=11.12 foot