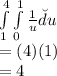Question

1. Let R be the equilateral in the xy plane with vertices (1,0), (4,0), (0,1) and (0,4) evaluate the double integral 1/(x+y) DA with the substation x=u-uv y=uv

Answer 1

Explanation:

Given that R is a treapezium with given vertices in the xy plane with side 3 units.

Substitution is

`x=u-uv\\y=uv`

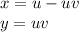
`J =\left[\begin{array}{ccc}x_u&x_v\\y_u&y_v\\\end{array}\right] \\=1-v      v\\   -u      u\\=u-uv+uv =u\\`

Hence dx dy = ududv

Integrand =
`(1)/(x+y) =(1)/(u)`

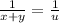
Limits now we have to change

We see from the vertices the line x+y changes from 1 to 4, i.e. 1<u<4 and

we get
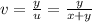`v=(y)/(u) =(y)/(x+y)` so v varies from 0 to 1

The given integral

=
`\int\limits^4_1\int\limits^1_0  {(1)/(u) } \u du\\ =(4)(1)\\=4`