Answer:
The area enclosed by given curves is
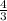 square units.
square units.
Explanation:
The given equation are
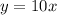
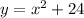
Draw the graph of both equation.
From the below graph it is clear that the graph intersect each other at (4,40) and (6,60).
The area of region enclosed by curves is
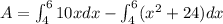
![A=10((1)/(2)[x^2]_(4)^(6))-(1)/(3)[x^3]_(4)^(6)-24[x]_(4)^(6)](https://img.qammunity.org/2020/formulas/mathematics/college/gkr88ualm1lgaweg3tjpcd8zenav4uh77r.png)
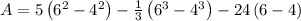
![A=5[20]-(1)/(3)[152]-24[2]](https://img.qammunity.org/2020/formulas/mathematics/college/rbehr06vllhne3effmae8jdhonqvt4rqpf.png)

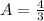
Therefore the area enclosed by given curves is
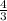 square units.
square units.