Question

The diffusion of oxygen (O2) through living tissue is often first approximated as the diffusion of

dissolved O2 in liquid water. Estimate the diffusion of O2 in water by the Wilke-Chang correlation
at 37℃.

Answer 1

Step-by-step explanation:

We assume that
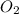`O_(2)` is represented by A and
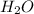`H_(2)O` is represented by B respectively.

According to Wilke Chang equation as follows.

`D_(AB) = (7.4 * 10^(-8) * (\phi_(B) M_(B))^(1/2) * T)/(V^(0.6)_(A) * \mu_(B))`

`D_{O_(2) - H_(2)O} = \frac{7.4 * 10^(-8) * (\phi_{H_(2)O} M_{H_(2)O})^(1/2) * T}{V^(0.6)_{O_(2)} * \mu_{H_(2)O}}`

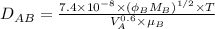
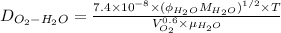
where, T = absolute temperature = (273 + 37)K = 310 K

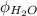`\phi_{H_(2)O}` = an association parameter for solvent water = 2.26

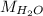`M_{H_(2)O}` = Molecular weight of water = 18 g/mol

`\mu` = viscosity of water (in centipoise) = 0.62 centipoise

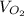`V_{O_(2)}` = the molar volume of oxygen = 25.6
`cm^(3)/g mol`

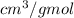
Hence, putting the given values into the above formula as follows.

`D_{O_(2) - H_(2)O} = \frac{7.4 * 10^(-8) * (\phi_{H_(2)O} M_{H_(2)O})^(1/2) * T}{V^(0.6)_{O_(2)} * \mu_{H_(2)O}}`

=
`\frac{7.4 * 10^(-8) * (2.26 * 18)^(1/2) * 310 K}{(25.6)^(0.6)_{O_(2)} * 0.692}`

=
`3021.7 * 10^(-8) cm^(2)/s`

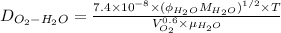
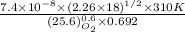
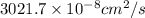
Thus, we can conclude that the diffusion of
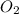`O_(2)` in water by the Wilke-Chang correlation at
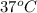`37^(o)C`.