Question

What is the maximum height of the basketball when the player passes the ball to someone? Initially, the ball moves at a speed of 12m/sec at an angle with respect to the horizontal of 45 degrees. Is it possible that other player standing 8m away is able to catch the ball without any bounces?

Answer 1

Answer with explanation:

Since the motion of the ball is projectile motion we shall use the equations for projectile motion.

The maximum height achieved by the projectile is given by

`h_(max)=(v_(o)^(2)sin^(2)(\theta ))/(2g)`

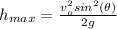
Applying the values we get

`h_(max)=(12^(2)* sin^(2)(45))/(2* 9.81)\\\\h_(max)=3.669m`

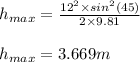
The range of the projectile is given by

`R=(v_(o)^(2)sin(2\theta ))/(2g)`

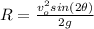
Applying values we get

`R=(12^(2)* sin(2* 45 ))/(2* 9.81)\\\\R=7.339m`

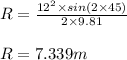
thus the maximum horizontal distance reached by the ball equals 7.339 meters after which it bounces thus a person standing 8 meters away will not be able to catch it.

(The height of the players is not taken into account since no info is given about their height.)