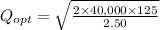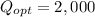Question

Annual demand for a product is 40,000 units. The product is used at a constant rate over the 365 days the company is open every year. The annual holding cost for the product is estimated to be $2.50 per unit and the cost of placing each order is $125.00. If the company orders according to the economic order quantity (EOQ) formula, then its optimal order size for this product would be:

Answer 1

The optimal order size would be 2,000

Step-by-step explanation:

The Economic Orded Quantity minimize the cost of inventory, considering the annual demand, the cost of holding the inventory in the company and the cost for each order.

`Q_(opt) = \sqrt{(2DS)/(H)}`

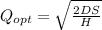
D = annual demand =40,000

S= setup cost = ordering cost =125

H= Holding Cost =2.50

`Q_(opt) = \sqrt{(2*40,000*125)/(2.50)}`

`Q_(opt) =2,000`