Question

A rectangular box has dimensions 4 by 5 by 2 . Increasing each dimension of the box by the same amount yields a new box with volume six times the old. Use the ALEKS graphing calculator to find how much each dimension of the original box was increased to create the new box. Round your answer to two decimal places.

Answer 1

2.68 units

Explanation:

We are given that a rectangular box has dimensions 4 by 5 by 2.

We have to find that how much each dimension of the original box was increased to create the new box

Let x be the increased value in each dimension

We know that volume of rectangular box=lbh

Volume of original box=
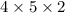`4* 5* 2`=40 cubic units

Volume of new box =
`6* 40=240 cubic units`

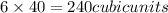
Dimension of new box=
`(x+4)(5+x)(2+x)`

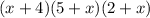
Volume of new box=240

`(x+5)(x+4)(x+2)=240`

`x^3+11x^2+38x+40-240=0`

`x^3+11x^2+38x-200=0`

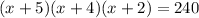
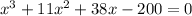
By graph we get

x=2.679

Round to two decimal places then we get

x=2.68

Hence, each dimension was increased by 2.68 units