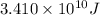Question

How much energy is produced in the creation of 5 grams of "O by the process: (10 pts.) 14N + α. 'H + 170 ("N-14.00307 gmole, α-4.0026 gmol, 'H 1.00783 g/mole, 170-| 6.999 13 g/mol)

Answer 1

Answer : The energy produced is
`3.410* 10^(10)J`

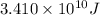
Explanation :

First we have to calculate the moles of
`^(17)O`.

`\text{Moles of }^(17)O=\frac{\text{Mass of }^(17)O}{\text{Molar mass of }^(17)O}=(5g)/(16.99913g/mole)=0.294133moles`

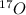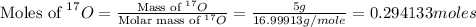
Now we have to calculate the mass defect.

The balanced reaction is,

`^(14)N+\alpha \rightarrow ^1H+^(17)O`

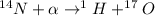
Mass defect = Sum of mass of product - sum of mass of reactants

`\Delta m=[(n_(^1H)* M_(^1H))+(n_(^(17)O)* M_(^(17)O))]-[(n_(^(14)N)* M_(^(14)N))+(n_(\alpha)* M_(\alpha))]`

where,

n = number of moles = 0.294133 moles

M = molar mass

Now put all the given values in the above, we get:

`\Delta m=[(n_(^1H)* M_(^1H))+(n_(^(17)O)* M_(^(17)O))]-[(n_(^(14)N)* M_(^(14)N))+(n_(\alpha)* M_(\alpha))]`

`\Delta m=[(0.294133mole* 1.00783g/mole)+(0.294133mole* 16.99913g/mole)]-[(0.294133mole* 14.00307g/mole)+(0.294133mole* 4.0026g/mole)]`

`\Delta m=0.00037943157g=3.7943157* 10^(-7)kg`

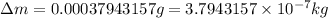
Now we have to calculate the energy produced.

`Energy=\Delta m* (c)^2`

`Energy=(3.7943157* 10^(-7)kg)* (299792458m/s)^2`

`Energy=3.410* 10^(10)J`

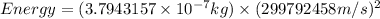
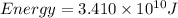
Therefore, the energy produced is
`3.410* 10^(10)J`