Answer:
Angle of refraction = 26.12°, time taken = 0.89 ns
Step-by-step explanation:
Using Snell's law as:
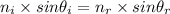
Where,
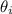 is the angle of incidence ( 41.0° )
is the angle of incidence ( 41.0° )
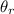 is the angle of refraction ( ? )
is the angle of refraction ( ? )
 is the refractive index of the refraction medium (glass, n=1.49)
is the refractive index of the refraction medium (glass, n=1.49)
 is the refractive index of the incidence medium (air, n=1)
is the refractive index of the incidence medium (air, n=1)
Hence,

Angle of refraction= sin⁻¹ 0.4403 = 26.12°.
Also,
The distance it has to travel = 20.0 cm × cos 26.12° = 17.9575cm
Also,
Refractive index is equal to velocity of the light 'c' in empty space divided by the velocity 'v' in the substance.
Or ,
n = c/v.
Speed of light in vacuum = 3×10¹⁰ cm/s
Speed in the medium is:
v = c/n = 3×10¹⁰ cm/s / 1.49 = 2.0134×10¹⁰ cm/s
The time taken is:
t = d/s = 17.9575 cm / 2.0134×10¹⁰ cm/s = 8.92×10⁻¹⁰ s ≅ 0.89×10⁻⁹ s
Also,
1 ns = 10⁻⁹ s
So, time taken = 0.89 ns