Question

Find the Vertex (h, x) using this formula

h space equals space minus fraction numerator b over denominator 2 a end fraction o f space f left parenthesis x right parenthesis space equals space minus 2 x to the power of 2 space end exponent plus space 4 x space minus space 7 space

(1, 5)

(-1, 5)

(1, -5)

(2, -7)

Answer 1

The correct option is C.

Explanation:

If a parabola is defined as

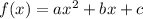`f(x)=ax^2+bx+c` .... (1)

then the vertex of the parabola is

`Vertex=(-(b)/(2a),f(-(b)/(2a)))`

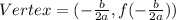
The given function is

`f(x)=-2x^2+4x-7` .... (2)

From (1) and (2) it is clear that

`a=-2,b=4,c=7`

`h=-(b)/(2a)`

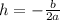
Substitute a=-2 and b=4 in the above equation.

`h=-(4)/(2(-2))=-(4)/(-4)=1`

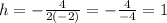
The value of h is 1.

substitute h=1 in function (2).

`f(1)=-2(1)^2+4(1)-7=-5`

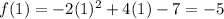
The vertex of the function is (1,-5). Therefore the correct option is C.