Question

Hugo and Viviana work in an office with ten other coworkers. Out of these 12 workers, their boss needs to choose a group of five to work together on a project. Suppose Hugo and Viviana absolutely refuse, under any circumstances, to work together. Under this restriction, how many different working groups of five can be formed?

Answer 1

Answer: There are 252 different working groups of five that can be formed.

Explanation:

Since we have given that

Number of workers = 12

Number of group of people to work together on a project = 5

Since Hugo and Viviana absolutely refuse, under any circumstances, to work together.

So, remaining number of workers = 12-2=10

so, we need to find the number of different groups of five that can be formed.

We will use "Combination":

`^(10)C_5\\\\=252`

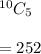
Hence, there are 252 different working groups of five that can be formed.