Answer:
0.0226 T, 7.096 V
Step-by-step explanation:
N = 600
l = 10 cm = 0.1 m
i = 3 A
diameter = 2 cm
The magnetic field on the axis is given by
B = μo x n x i
where, n be the number of turns per unit length, i be the current and μo be the permeability of free space.
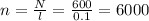
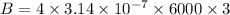
B = 0.0226 T
time taken to decrease the magnetic field to be zero is t = 0.001 second
Let e be the amount of voltage induced.
According to the Faraday's law of electromagnetic induction
e = rate of change of magnetic flux
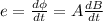
where, A be the area of coil
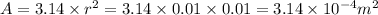
So, induced voltage
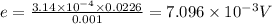
e = 7.096 mV