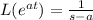Question

Use the Laplace transformation to solve the given IVP.

y'-y=2sin3t, y(0)=0

Answer 1

`y(t)=(3)/(5)e^t-(3)/(5)cost 3t-(1)/(5) sin3t`

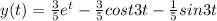
Explanation:

We are given that

y'-y=2 sin3t,y(0)=0

We have to solve given differential equation using Laplace transform

We know that L(y'-y)=L(2sin3t)

`sY(s)-y(0)-Y(s)= (6)/(s^2+9)`

`L(sinat)=(a)/(s^2+a^2)`

`Y(s)(s-1)=(6)/(s^2+9)`

`Y(s)=(6)/((s^2+9)(s-1))`

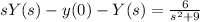
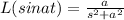
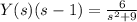
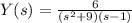
Using partial fraction

`(6)/((s^2+9)(s-1))=(A)/(s-1)+(Bs+c)/(s^2+9)`

`6=A(s^2+9)+(s-1)(Bs+C)`

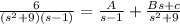
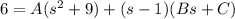
s-1=0 then s=1

substitute s= 1 in equation

6=A(1+9)

`A=(6)/(10)=(3)/(5)`

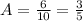
Comparing coefficient of
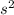`s^2` and s on both sides then we get

`A+B=0`

`B=-A=-(3)/(5)`

`-B+C=0`

`B=C=-(3)/(5)`

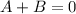
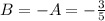
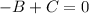
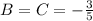
Substitute the values

Then, Y(s)=
`(3)/(5)(1)/(s-1)+((-3)/(5) s-(3)/(5))/(s^2+9)`

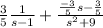
Apply inverse transform then we get

`y(t)=(3)/(5)e^t-(3)/(5)cost 3t-(1)/(5) sin3t`

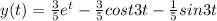
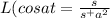`L(cos at}=(s)/(s^+a^2)` and
`L(e^(at))=(1)/(s-a)`