Question

You have 3 dice. For each die: Three sides are painted vellow, two sides are painted red, and one side is painted blue. If the three dice are rolled, what is the probability that they all land with the same color facing up? 1 (b) 6 1 (e) 15 (a) (c (d)

Answer 1

The probability that they all land with the same color facing up is 1/6.

Explanation:

Total number of dice = 3

Number of yellow sides in each dice = 3

Number of Red sides in each dice = 2

Number of Blue sides in each dice = 1

Let Y= Yellow color facing up, R= Red color facing up, B= Blue color facing up

`P(Y)=(3)/(6)=(1)/(2)`

`P(R)=(2)/(6)=(1)/(3)`

`P(B)=(1)/(6)`

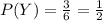
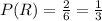
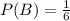
We need to find the probability that they all land with the same color facing up.

P(All dice land with the same color facing up) = P(All dice land with Yellow color facing up) + P(All dice land with Red color facing up) + P(All dice land with Blue color facing up)

`P(\text{Same color})=(1)/(2)\cdot (1)/(2)\cdot (1)/(2)+(1)/(3)\cdot (1)/(3)\cdot (1)/(3)+(1)/(6)\cdot (1)/(6)\cdot (1)/(6)`

`P(\text{Same color})=(1)/(8)+(1)/(27)+(1)/(216)`

`P(\text{Same color})=(27+8+1)/(216)`

`P(\text{Same color})=(1)/(6)`

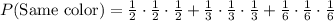
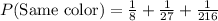
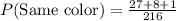
Therefore the probability that they all land with the same color facing up is 1/6.

Answer 2

Answer:
`(1)/(6)`

Explanation:

Given : You have 3 dice. For each die: Three sides are painted yellow, two sides are painted red, and one side is painted blue.

The probability of getting yellow side on any dice =
`(3)/(6)=(1)/(2)`

The probability of getting red side on any dice =
`(2)/(6)=(1)/(3)`

The probability of getting blue side on any dice =
`(1)/(6)`

Now, If the three dice are rolled, then the probability that they all land with the same color facing up will be :-

`((1)/(2))^3+((1)/(3))^3+ ((1)/(6))^3\\\\=(1)/(8)+(1)/(81)+(1)/(216)=(1)/(6)`

Hence, the probability that they all land with the same color facing up =
`(1)/(6)`