Question

Differentiate 3sinx + 4(cosx)^3

Answer 1

We can differentiate the two terms separately, since we have

`[f(x)+g(x)]' = f'(x)+g'(x)`

The first term comes in the form
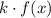`k\cdot f(x)`, where
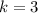`k=3` and
`f(x)=\sin(x)`

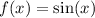
So, we have

`[k\cdot f(x)]' = kf'(x)`

The derivative of sine is cosine, so we have

`[3\sin(x)]' = 3\cos(x)`

And the first term is done. For the second term, we have to use the power rule

`[f^n(x)]' = nf^(n-1)(x)\cdot f'(x)`

Since the derivative of cosine is negative sine, we have

`[4\cos^3(x)]'= 4\cdot 3\cos^2(x)(-\sin(x)) = -12\cos^2(x)\sin(x)`

So, the whole derivative is the sum of the derivatives of the two terms, and we have

`[3\sin(x) + 4\cos^3(x)]'=3\cos(x)-12\cos^2(x)\sin(x)`