Step-by-step explanation:
Bernoulli equation for the flow between bottom of the tank and pipe exit point is as follows.
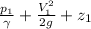 =
=
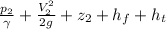
![((100 * 144))/(62.43) + 0 + h[tex] = [tex]((50 * 144))/((62.43)) + ((70)^(2))/(2(32.2)) + 0 + 40 + 60](https://img.qammunity.org/2020/formulas/chemistry/college/15d37lbft9z38kttm61enopclmo17y5n38.png)
h =
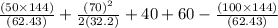
= 60.76 ft
Hence, formula to calculate theoretical power produced by the turbine is as follows.
P = mgh
=
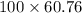
= 6076 lb.ft/s
= 11.047 hp
Efficiency of the turbine will be as follows.
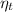 =
=
 × 100%
× 100%
=
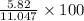
= 52.684%
Thus, we can conclude that the efficiency of the turbine is 52.684%.