Question

An environmental scientist wanted to test if the mean concentration of carbon trioxide in blue water exceeds the safe level of 22 blops per cubic centimeter of water. She collected 64 samples of blue water, and obtained a sample mean of 26.935 blops and a sample standard deviation of 14 blops. At significance level 0.05, can it be concluded that the true mean concentration exceeds 22 blops?

A and B are independent events

Answer 1

Answer with explanation:-

Let
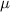`\mu` be the population mean.

By considering the given information , we have

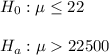`H_0:\mu\leq22\\\\H_a:\mu>22500`, since the alternative hypothesis is right tailed , so the test is right tail test.

Given : Sample size : n=64, which is a large sample (n>30) so we use z-test.

Sample mean :
`\overline{x}=26.935`

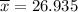
Then, Standard deviation :
`\sigma=14`

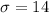
Test statistic for population mean :-

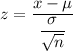
`z=\frac{\overlien{x}-\mu}{(\sigma)/(√(n))}`

i.e.
`z=(26.935-22)/((14)/(√(64)))=2.82`

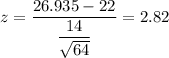
P-value =
`P(z>2.82)=1-P(z<2.82)=1- 0.9975988= $$0.0024012`

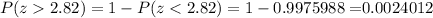
Since the p-value is less than the significance level , so we reject the null hypothesis that mean we can accept the alternative hypothesis.

Thus , we conclude that the true mean concentration can exceeds 22 blops .