Question

P(x)-x15x-48x + 450, x è 3 is an approximation to the total profit (in thousands of dollars) from the sale of x hundred thousand tires. Find the number of hundred thousands of tires that must be sold to maximize profit. O A. 5 hundred thousand B. 3 hundred thousand O C. 8 hundred thousand 0 D. 10 hundred thousand

Answer 1

Answer: C. 8 hundred thousand

Step-by-step explanation:

Assuming the given profit function is:

`P(x) =- x^3+15x^2-48x+450`

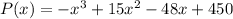
Then we differentiate:

`P'(x)=-3x^2+30x-48`

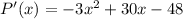
And we set the derivative equal to 0 and solve the resulting equation in order to get the critical points:

`-3x^2+30x-48=0`

Divide by -3 the equation:

`x^2-10x+16=0`

Factor:

`(x-8)(x-2)=0`

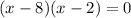
Set each factor equal to zero and solve:

`x-8=0\to x=8`

`x-2=0\to x=2`

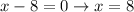
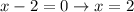
Then we check which is the maximum by using the first derivative test.

Into the derivative, let’s plug x=0 which is a value in the interval before the critical point x=2:

`P'(0)=-3(0)^2+30(0)-48=-48`

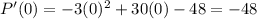
The derivative is negative, so the profit function is decreasing before x=2

Into the derivative, let’s plug x=3 which is a value in the interval after the critical point x=2 and before the critical point x=8:

`P'(3)=-3(3)^2+30(3)-48=15`

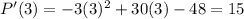
The derivative is positive, so the profit function is increasing between x=2 and x=8

Notice then at x=2 we have a local minimum since the function changed from decreasing to increasing there.

Into the derivative, let’s now plug x=10 which is a value in the interval after the critical point x=8:

`P'(10)=-3(10)^2+30(10)-48=-48`

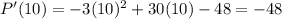
The derivative is negative, so the profit function is decreasing after x=8.

Therefore, at x=8 we have a local maximum because the function changed from increasing to decreasing there.

So, the solution is x=8, meaning 8 hundred thousand tires must be sold to maximize profit. That is option C.