Question

On an exam, the mean score is 78 points, with a standard deviation of 6 points. Assuming normal distribution of the scores, approximately what percentage of students received more than 85?A.12% B.17% C.8% D.9% E.None of the above

Answer 1

Answer: A. 12%

Step-by-step explanation:-

Given : In an exam , Mean score :
`\mu=78\text{ points}`

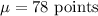
Standard deviation :
`6\text{ points}`

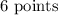
Let X be a random variable that represents the scores of students.

We assume that the points are normally distributed.

Z-score :
`z=(x-\mu)/(\sigma)`

For x = 85, we have

`z=(85-78)/(6)\approx1.17`

Then using standard normal distribution table, the probability that the students received more than 85 is given by :-

`P(x>85)=P(z>1.17)=1-P(z<1.17)\\\\=1-0.8789995=0.1210005\approx0.12=12\%`

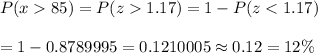
Hence, the percentage of students received more than 85 =12%