Answer:
Difference in the angle of refraction = 0.3°
41.04° is the minimum angle of incidence.
Step-by-step explanation:
Angle of incidence = 38.0°
For yellow light :
Using Snell's law as:
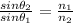
Where,
Θ₁ is the angle of incidence
Θ₂ is the angle of refraction
n₁ is the refractive index for yellow light which is 1.523
n₂ is the refractive index of air which is 1
So,
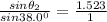

Angle of refraction for yellow light = sin⁻¹ 0.9377 = 69.67°.
For green light :
Using Snell's law as:
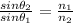
Where,
Θ₁ is the angle of incidence
Θ₂ is the angle of refraction
n₁ is the refractive index for green light which is 1.526
n₂ is the refractive index of air which is 1
So,
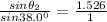

Angle of refraction for green light = sin⁻¹ 0.9395 = 69.97°.
The difference in the angle of refraction = 69.97° - 69.67° = 0.3°
Calculation of the critical angle for the yellow light for the total internal reflection to occur :
The formula for the critical angle is:
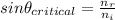
Where,
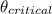 is the critical angle
is the critical angle
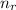 is the refractive index of the refractive medium.
is the refractive index of the refractive medium.
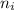 is the refractive index of the incident medium.
is the refractive index of the incident medium.
n₁ is the refractive index for yellow light which is 1.523 (incident medium)
n₂ is the refractive index of air which is 1 (refractive medium)
Applying in the formula as:
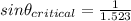
The critical angle is = sin⁻¹ 0.6566 = 41.04°