Answer:
The correct answer is option 'c': 30 AUs
Step-by-step explanation:
For a spherical wave front emitted by sun with total energy 'E' the energy density over the surface when it is at a distance 'r' from the sun is given by
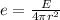
This energy per unit area is sensed by observer as intensity of the sun.
Let the initial intensity of sun at a distance
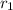 be
be
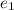
Thus if the sun becomes 900 times dimmer we have
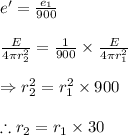
Thus the distance increases 30 times.