Question

A certain elastic conducting material is stretched into a circular loop of 1.6 cm radius. It is placed with its plane perpendicular to a uniform 0.8 T magnetic field. When released, the radius of the loop starts to shrink at an instantaneous rate of 75.0cm/s. What emf is induced in the loop at that instant in units of V?

Answer 1

Induced emf in the loop is 0.0603 volts.

Step-by-step explanation:

It is given that,

Radius of the circular loop, r = 1.6 cm = 0.016 m

Magnetic field, B = 0.8 T

When released, the radius of the loop starts to shrink at an instantaneous rate of 75.0 cm/s,
`(dr)/(dt)=75\ cm/s=0.75\ m/s`

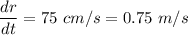
We need to find the magnitude of induced emf at that instant. Induced emf is given by :

`\epsilon=(-d\phi)/(dt)`

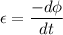
Where

`\phi` is the magnetic flux,
`\phi=B* A`

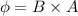
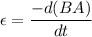`\epsilon=(-d(BA))/(dt)`, A is the area of cross section

`\epsilon=-(-d(B(\pi r^2)))/(dt)`

`\epsilon=-2\pi r B((dr)/(dt))`

`\epsilon=-2\pi * 0.016* 0.8 * 0.75\ m/s`

`\epsilon=0.0603\ V`

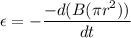
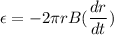
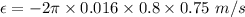
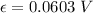
So, the induced emf in the loop is 0.0603 volts. Hence, this is the required solution.