Question

A red laser from the physics lab is marked as producing 632.8-nm light. When light from this laser falls on two closely spaced slits, an interference pattern formed on a wall several meters away has bright red fringes spaced 5.50 mm apart near the center of the pattern. When the laser is replaced by a small laser pointer, the fringes are 5.62 mm apart. What is the wavelength of light produced by the pointer?

Answer 1

646.60 nm

Explanation:

Given:

wavelength of the light produced, λ₁ = 632.8 nm

Spacing between the bright fringes, y₁ = 5.50 mm

Spacing between the bright fringes when the laser is replaced,y₂ = 5.62 nm

Now,

the spacing between the bright fringes (y) is given as:

y =
`wavelength* (D)/(d)`

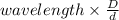
where,

D is the distance between the slit and the screen

d is the distance between the slits

or

`(D)/(d) = (y)/(\lambda)`

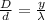
therefore, using the above relation, we have

`(y_1)/(\lambda_1)=(y_2)/(\lambda_2)`

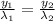
where,

λ₂ is the wavelength of the light produced by the smaller pointer

thus, on substituting the values,we get

`(5.50)/(632.8)=(5.62)/(\lambda_2)`

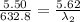
or

λ₂ = 646.60 nm

Hence,

the wavelength of light produced by the smaller pointer = 646.60 nm