Question

An ideal gas (C}R), flowing at 4 kmol/h, expands isothermally at 475 Kfrom 100 to 50 kPa through a rigid device. If the power produced is 2000 W, what is the corresponding rate of heat flow? What is the rate of lost work?

Answer 1

Answer: The rate of heat flow is 3.038 kW and the rate of lost work is 1.038 kW.

Step-by-step explanation:

We are given:

`C_p=(7)/(2)R\\\\T=475K\\P_1=100kPa\\P_2=50kPa`

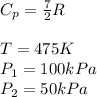
Rate of flow of ideal gas , n = 4 kmol/hr =
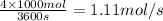`(4* 1000mol)/(3600s)=1.11mol/s` (Conversion factors used: 1 kmol = 1000 mol; 1 hr = 3600 s)

Power produced = 2000 W = 2 kW (Conversion factor: 1 kW = 1000 W)

We know that:

`\Delta U=0` (For isothermal process)

So, by applying first law of thermodynamics:

`\Delta U=\Delta q-\Delta W`

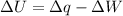
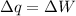`\Delta q=\Delta W` .......(1)

Now, calculating the work done for isothermal process, we use the equation:

`\Delta W=nRT\ln ((P_1)/(P_2))`

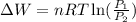
where,

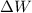`\Delta W` = change in work done

n = number of moles = 1.11 mol/s

R = Gas constant = 8.314 J/mol.K

T = temperature = 475 K

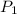`P_1` = initial pressure = 100 kPa

`P_2` = final pressure = 50 kPa

Putting values in above equation, we get:

`\Delta W=1.11mol/s* 8.314J* 475K* \ln ((100)/(50))\\\\\Delta W=3038.45J/s=3.038kJ/s=3.038kW`

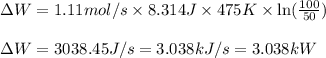
Calculating the heat flow, we use equation 1, we get:

[ex]\Delta q=3.038kW[/tex]

Now, calculating the rate of lost work, we use the equation:

`\text{Rate of lost work}=\Delta W-\text{Power produced}\\\\\text{Rate of lost work}=(3.038-2)kW\\\text{Rate of lost work}=1.038kW`

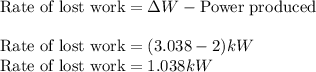
Hence, the rate of heat flow is 3.038 kW and the rate of lost work is 1.038 kW.