Step-by-step explanation:
As it is given that no heat is generating and the system is present in steady state.
As we know that,
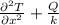 =
=
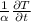
So, according to the given conditions,
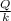 = 0, and
= 0, and
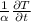 = 0
= 0
So,
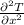 = 0 ,
= 0 ,
 =
=
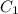
T =
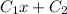
Hence, boundary conditions will be as follows.
At x = 0, T =
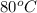
At x = L, T =

Applying boundary condition is
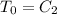
Therefore,
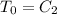 =
=
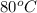
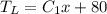
40 =
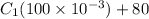
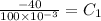
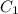 = -400
= -400
Hence, temperature distribution in a block will be as follows.
T = -400x + 80
At center, x =
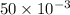
Therefore, T =
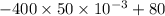
=
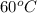
Thus, we can conclude that the temperature of block at the center point is
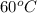 .
.