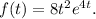Question

(with steps please) Find the inverse Laplace transform, f(t), of the function: 16/(s-4)^3

Answer 1

Answer: The required inverse transform of the given function is

`f(t)=8t^2e^(4t).`

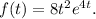
Step-by-step explanation: We are given to find the inverse Laplace transform, f(t), of the following function :

`F(s)=(16)/((s-4)^3).`

We have the following Laplace formula :

`L\{t^ne^(at)\}=(n!)/((s-a)^(n+1))\\\\\\\Rightarrow L^(-1)\{(1)/((s-a)^(n+1))\}=(t^ne^(at))/(n!).`

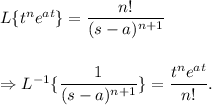
Therefore, we get

`f(t)\\\\=L^(-1)\{(16)/((s-4)^3)\}\\\\\\=16*\frac{t^{3-1e^(4t)}}{(3-1)!}\\\\\\=(16)/(2)t^2e^(4t)\\\\\\=8t^2e^(4t).`

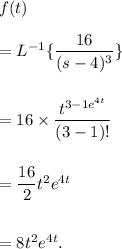
Thus, the required inverse transform of the given function is

`f(t)=8t^2e^(4t).`