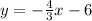Question

Determine the slope-intercept form of the equation of the line parallel to y = - 4/3 x + 11 that passes through the point (–6, 2).

Answer 1

`y = -(4)/(3)x -6`

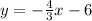
Explanation:

If two lines are parallel then they have the same slope.

The slope-intercept form of a line is as follows:

`y = mx + b`

Where m is the slope of the line and b is the intersection with the y axis.

In this case we have the following line:

`y = -(4)/(3)x + 11`

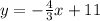
Note that the slope of the line is:

`m=-(4)/(3)`

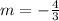
Therefore a line parallel to this line will have the same slope
`m=-(4)/(3)`

`y = -(4)/(3)x + b`

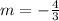
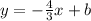
To find the value of the constant b we substitute the point given in the equation of the line and solve for b. Because we know that this line goes through that point

`2 = -(4)/(3)(-6) + b`

`2 = 8 + b`

`b=-6`

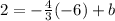
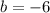
Finally the equation is:

`y = -(4)/(3)x -6`

Answer 2

`\large\boxed{y=-(4)/(3)x-6}`

Explanation:

The slope-intercept form of an equation of a line:

Put the coordinates of the given point (-6, 2) to the equation:

`2=-(4)/(3\!\!\!\!\diagup_1)(-6\!\!\!\!\diagup^2)+b`

`2=(4)(2)+b`

`2=8+b` subtract 8 from both sides

`-6=b\to b=-6`

Finally:

`y=-(4)/(3)x-6`