Answer: A) 0.0480 grams and B) 56.16 years.
Explanation: Half live is the time in which the amount of radioactive substance remains halve of its initial amount.
The formula we use for solving this type of problem is:
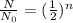
where,
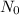 is the initial amount and N is the remaining amount of radioactive substance and n is the number of half lives.
is the initial amount and N is the remaining amount of radioactive substance and n is the number of half lives.
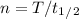
where, T is the time and
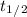 is half life.
is half life.
A) from given data,
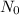 = 2 g
= 2 g
T = 70 years
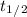 = 13 years
= 13 years
N= ?
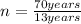
n = 5.38
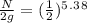
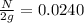
N = 0.0480 g
So, 0.0480 grams of the substance will be remaining after 70 years.
B)
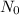 = 2 g
= 2 g
N = 0.1 g
T = ?
Let's first calculate the value of n for this.
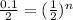
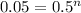
Taking log to both sides:
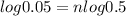
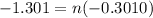

n = 4.32
Half life is 13 years, so we can calculate the time as:
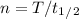
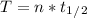
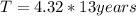
T = 56.16 years
So, it will take 56.16 years for the radioactive substance to decay from 2 g to 0.1 g.