Answer: After 4.55 hours the ships will be nearest to each other, and this distance would be 54.54 km.
Explanation:
Since we have given that
Distance between ship A and ship B = 100 km
Speed at which Ship A is sailing west = 12 km/hr
Speed at which Ship B is sailing south = 10 km/hr
Since they are sailing opposite to each other, so their relative speed would be
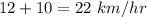
So, Time taken is given by
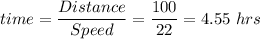
Distance would be

Hence, After 4.55 hours the ships will be nearest to each other, and this distance would be 54.54 km.